Xác định giao tuyến của hai mặt phẳng - Toán 11
Bài toán xác định giao tuyến của hai mặt phẳng, tìm giao điểm của đường
thẳng và mặt phẳng; xác định thiết diện là những bài toán cơ bản của Hình
học không gian - Toán 11. Trong bài viết này thầy sẽ hướng dẫn từng
dạng toán kể trên để các em có phương pháp giải quyết trong các bài tập
trên lớp.
VẤN ĐỀ 1. Xác định giao tuyến của hai mặt phẳng
Phương pháp giải: Muốn tìm giao tuyến của hai mặt phẳng ta có thể tìm hai điểm chung phân biệt của hai mặt phẳng. Khi đó giao tuyến là đường thẳng đi qua hai điểm chung đó.
Ví dụ 1. Cho hình chóp S.ABCD. Đáy ABCD có AB cắt CD tại E, AC cắt BD tại
F.
a) Tìm giao tuyến của các cặp mặt phẳng (SAB) và (SCD), (SAC) và
(SBD).
b) Tìm giao tuyến của (SEF) với các mặt phẳng (SAD), (SBC).
Giải
+ (SAB) và (SCD) có điểm S chung.
Ngoài ra, AB $\cap$ CD = E.
E $\in$ AB, AB $\subset$ (SAB) $\Leftrightarrow$ E $\in$ (SAB).
tương tự, E $\in$ CD, CD $\subset$ (SCD) $\Leftrightarrow$ E $\in$
(SCD).
Do đó (SAB) và (SCD) có điểm E chung.
Vậy (SAB) và (SCD) có giao tuyến là đường thẳng SE.
+ Tìm giao tuyến của các cặp mặt phẳng (SAC) và (SBD).
(SAC) và (SBD) có điểm S chung.
Ngoài ra, AC $\cap$ BD = F.
F $\in$ AC, AC $\subset$ (SAC) $\Leftrightarrow$ F $\in$ (SAC).
tương tự, F $\in$ BD, BD $\subset$ (SBD) $\Leftrightarrow$ F $\in$
(SBD).
Do đó (SAC) và (SBD) có điểm F chung.
Vậy (SAC) và (SBD) có giao tuyến là đường thẳng SF.
b)
+ Tìm giao tuyến của (SEF) với mặt phẳng (SAD).
(SEF) và (SAD) có điểm S chung.
Gọi EF $\cap$ AD = N.
N $\in$ AD, AD $\subset$ (SAD) $\Leftrightarrow$ N $\in$ (SAD).
tương tự, N $\in$ EF, EF $\subset$ (SEF) $\Leftrightarrow$ N $\in$
(SEF).
Do đó (SEF) và (SAD) có điểm N chung.
Vậy (SEF) và (SAD) có giao tuyến là đường thẳng SN.
+ Tìm giao tuyến của (SEF) với mặt phẳng (SAD).
(SEF) và (SAD) có điểm S chung.
Gọi EF $\cap$ BC = M.
M $\in$ BC, BC $\subset$ (SBC) $\Leftrightarrow$ M $\in$ (SBC).
tương tự, M $\in$ EF, EF $\subset$ (SEF) $\Leftrightarrow$ M $\in$
(SEF).
Do đó (SEF) và (SBC) có điểm M chung.
Vậy (SEF) và (SBC) có giao tuyến là đường thẳng SM.
Bài tập đề nghị
Bài 1. Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành tâm O. M, N, P
lần lượt là trung điểm của BC, CD, SO. Tìm giao tuyến của mp(MNP) với các
mặt phẳng (SAB), (SAD), (SBC) và (SCD).
Bài 2. Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AD và
BC.
a) Tìm giao tuyến của 2 mặt phẳng (IBC) và (JAD).
b) M là một điểm trên cạnh AB, N là một điểm trên cạnh AC. Tìm giao tuyến
của 2 mặt phẳng (IBC) và (DMN).
VẤN ĐỀ 2: Tìm giao điểm của đường thẳng (d) và mặt phẳng (P)
Phương pháp giải
Trường hợp 1. Trong mp(P) có sẵn đường thẳng d' cắt d tại I.
Ta có ngay d $\cap$ (P) = I.
Trường hợp 2. Trong mp(P) không có sẵn đường thẳng d' cắt d. Khi đó ta thực hiện như sau:
- Chọn mặt phẳng phụ (Q) chứa d và (Q) cắt (P) theo giao tuyến d'.
- Gọi I = d' $\cap$ d.
Ta có d $\cap$ (P) = I.
Ví dụ 2. Cho tứ diện ABCD. Trên AC và AD lần lượt lấy các điểm M, N sao
cho MN không song song với CD. Gọi O là một điểm bên trong tam giác
BCD.
a) Tìm giao tuyến của (OMN) và (BCD).
b) Tìm giao điểm của BC và BD với mặt phẳng (OMN).
Giải
a) Tìm giao tuyến của (OMN) và (BCD)
(OMN) và (BCD) có điểm O chung
Kéo dài MN và CD, gọi E = MN $\cap$ CD
E $\in$ MN, MN $\subset$ (OMN) $\Leftrightarrow$E $\in$ (OMN).
tương tự, E $\in$ CD, CD $\subset$ (BCD) $\Leftrightarrow$ E $\in$
(BCD).
Do đó (OMN) và (BCD) có điểm E chung.
Vậy (OMN) và (BCD) có giao tuyến là đường thẳng OE.
b) Gọi P = OE $\cap$ BC; Q = OE $\cap$ BD
+ Tìm giao điểm của BC với mặt phẳng (OMN). (Note: Từ hình vẽ ta thấy
không có đường thẳng nào trong mp(OMN) cắt BC, vậy ta thực hiện theo
trường hợp 2. Để đơn giản ta chọn mặt phẳng (Q) chính là mp(BCD) đã tìm
giao tuyến ở ý a))
Ta có BC $\subset$ (BCD)
(OMN) $\cap$ (BCD) = OE (ý a),
P = OE $\cap$ BC
Do đó: P = BC $\cap$ (OMN)
+ Tìm giao điểm của BD với mặt phẳng (OMN).
Ta có BD $\subset$ (BCD),
(OMN) $\cap$ (BCD) = OE (ý a),
Q = OE $\cap$ BD
Do đó: Q = BD $\cap$ (OMN)
Bài tập đề nghị
Bài 1. Cho tứ diện ABCD. M, N là hai điểm lần lượt trên AC và AD. O là
một điểm bên trong tam giác BCD. Tìm giao điểm của đường thẳng và mặt
phẳng dưới đây
a) MN và (ABO).
b) AO và (BMN).
Hướng dẫn:
a) Tìm giao tuyến của (ABO) và (ACD).
b) Tìm giao tuyến của (BMN) và (ABO).
Bài 2. Cho hình chóp S.ABCD, có đáy là hình thang ABCD, cạnh đáy lớn AB.
Gọi I, J, K là ba điểm lần lượt trên SA, AB, BC.
a) Tìm giao điểm của IK với (SBD).
b) Tìm các giao điểm của mặt phẳng (IJK) với SD và SC.
Hướng dẫn:
a) Tìm giao tuyến của (SBD) với (IJK).
b) Tìm giao tuyến của (IJK) với (SBD và (SCD).
VẤN ĐỀ 3: Xác định thiết diện của một hình chóp với một mặt phẳng
Định nghĩa. Thiết diện (hay mặt cắt) của hình (H) khi cắt bởi mặt phẳng (P) là phần chung nhau của mặt phẳng (P) và hình (H). Tìm thiết diện tức là tìm hình dạng mặt cắt này, thường là một đa giác như tam giác, tứ giác…
Phương pháp giải
Muốn xác định thiết diện của một hình chóp với mặt phẳng (P) ta thực hiện như sau:
Bước 1. Từ điểm chung có sẵn, xác định giao tuyến đầu tiên của (P) với một mặt của hình chóp (có thể là mặt phẳng trung gian).
Bước 2. Cho giao tuyến này cắt các cạnh của mặt đó của hình chóp, ta sẽ được các điểm chung mới của (P) với các mặt khác. Từ đó xác định được các giao tuyến mới với các mặt này.
Bước 3. Tiếp tục bước 2 cho tới khi các giao tuyến khép kín ta được thiết diện.
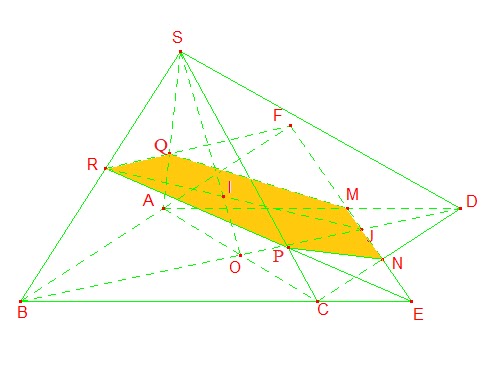
Ví dụ 3. Cho hình chóp S.ABCD, có đáy là hình bình hành tâm O. Gọi M, N,
I là ba điểm trên AD, CD, SO. Tìm thiết diện của hình chóp với mặt phẳng
(MNI).
Giải
(Note: Ở bước 1, Do M, N nằm trên AD và CD nên ta chọn mặt đáy (ABCD) để
xác định giao tuyến đầu tiên. Ngoài ra, điểm I nằm trên SO (không nằm trên
bất cứ mặt nào của hình chóp) nên ta chọn mặt phẳng phụ (SBD) để tìm điểm
chung mới.)
Ta có:
+ (MNI) và (ABCD) có hai điểm M, N chung nên (MNI) $\cap$ (ABCD) =
MN
+ (MNI) và (SBD) có điểm I chung
Gọi J = MN $\cap$ BD
J $\in$ MN, MN $\subset$ (MNI) $\Leftrightarrow$ J $\in$ (MNI).
tương tự, J $\in$ BD, BD $\subset$ (SBD) $\Leftrightarrow$ J $\in$
(SBD).
Do đó (MNI) và (SBD) có điểm J chung.
Vậy (MNI) $\cap$ (SBD) = IJ.
Trong (BCD) gọi R = IJ $\cap$ BD
Trong (ABCD) gọi E = MN $\cap$ BC, F = MN $\cap$ AB
+ (MNI) và (SBC) có hai điểm R và E chung nên (MNI) $\cap$ (SBC) =
RE
+ (MNI) và (SAB) có hai điểm R và F chung nên (MNI) $\cap$ (SAB) =
RF
Trong (SBC) gọi P = RE $\cap$ SC
Trong (SAB) gọi Q = RF $\cap$ SA
+ (MNI) và (SCD) có hai điểm N và P chung nên (MNI) $\cap$ (SCD) =
NP
+ (MNI) và (SAD) có hai điểm M và Q chung nên (MNI) $\cap$ (AD) =
MQ
Vậy thiết diện cần tìm là ngũ giác MNPRQ.
Bài tập đề nghị
Bài 1. Cho hình chóp S.ABCD. M là một điểm trên cạnh SC, N và P lần lượt
là trung điểm của AB và AD. Tìm thiết diện của hình chóp với mặt phẳng
(MNP).
Hướng dẫn: Thiết diện là 1 ngũ giác.
Bài 2. Cho hình chóp S.ABCD. Trong tam giác SBC lấy một M. Trong
tam giác SCD lấy điểm N.
a) Tìm giao điểm của MN và (SAC).
b) Tìm giao điểm của SC với (AMN).
c) Tìm thiết diện của hình chóp S.ABCD với mặt phẳng (AMN).
Hướng dẫn:
a) Tìm (SMN) $\cap$ (SAC)
b) Thiết diện là tứ giác.
Bài 3. Cho hình chóp S.ABCD, có đáy là hình bình hành tâm O. Gọi M, N, P
lần lượt là trung điểm của SB, SD và OC.
a) Tìm giao tuyến của (MNP) với (SAC), và giao điểm của (MNP) với
SA.
b) Xác định thiết diện của hình chóp với (MNP).
Hướng dẫn:
b) Thiết diện là ngũ giác.
Bài 4. Cho hình chóp S.ABCD, có đáy là hình bình hành. Gọi M là trung
điểm của SB, G là trọng tâm tam giác SAD.
a) Tìm giao điểm I của GM với (ABCD). Chứng minh (CGM) chứa CD.
b) Chứng minh (CGM) đi qua trung điểm của SA. Tìm thiết diện của hình
chóp với (CGM).
c) Tìm thiết diện của hình chóp với (AGM).
Hướng dẫn:
b) Thiết diện là tứ giác
c) Tìm (AGM) $\cap$ (SAC). Thiết diện là tứ giác.
Bài 5. Cho hình chóp S.ABCD, M là một điểm trên cạnh BC, N là một điểm
trên cạnh SD.
a) Tìm giao điểm I của BN và (SAC) và giao điểm J của MN và (SAC).
b) DM cắt AC tại K. Chứng minh S, K, J thẳng hàng.
c) Xác định thiết diện của hình chóp S.ABCD với mặt phẳng (BCN).
Hướng dẫn:
a) Gọi O=AC $\cap$ BD thì I=SO $\cap$ BN, J=AI $\cap$ MN
b) J là điểm chung của (SAC) và (SDM)
c) Nối CI cắt SA tại P. Thiết diện là tứ giác BCNP.
Tham khảo thêm bài viết:
Tham khảo thêm bài viết: