Công thức cần ghi nhớ để tính thể tích đa diện - Toán 12
TỔNG HỢP CÔNG THỨC HÌNH HỌC CẦN NHỚ ĐỂ TÍNH THỂ TÍCH CHÓP
CÔNG THỨC TÍNH DIỆN TÍCH
1. HÌNH VUÔNG
Đối với hình vuông ABCD có cạnh là a
+) Diện tích: $S=a^2$
+) Độ dài đường chéo: $AC=a\sqrt{2}$
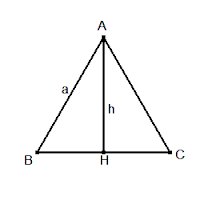
2. TAM GIÁC ĐỀU
Đối với tam giác đều ABC có cạnh là a thì
+) Diện tích: $\displaystyle S=\frac{a^2\sqrt{3}}{4}$
+) Độ dài đường cao: $\displaystyle AH=\frac{a\sqrt{3}}{2}$
3. HÌNH THOI
Đối với hình thoi ABCD thì diện tích:
$\displaystyle S=\frac{1}{2}AC.BD$ (nửa tích hai đường chéo)
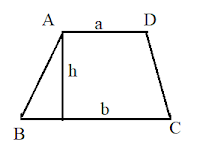
4. HÌNH THANG
Đối với hình thoi ABCD thì diện tích:
$S = \frac{{\left( {a + b} \right).h}}{2}$
B. CÔNG THỨC TÍNH CHIỀU CAO
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- ${b^2} = a.b'$; ${c^2} = a.c'$
- ${h^2}=b'.c'$
- $\frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}$
2. YẾU TỐ GÓC
- $\sin \alpha = \frac{cạnh đối}{cạnh huyền}$
- $\cos \alpha = \frac{cạnh kề}{cạnh huyền}$
- $\tan \alpha = \frac{cạnh đối}{cạnh kề}$
CÔNG THỨC THỂ TÍCH
CÔNG THỨC THỂ TÍCH HÌNH CHÓP
$\displaystyle V_{chóp}=\frac{1}{3}S.h$
Trong đó S là diện tích đáy của hình
chóp, h là chiều cao của hình chóp
CÔNG THỨC THỂ TÍCH HÌNH TRỤ
$\displaystyle V_{trụ}=S.h$
Trong đó S là diện tích đáy của hình trụ, h là chiều cao của hình trụ
Trong đó S là diện tích đáy của hình trụ, h là chiều cao của hình trụ
Tham khảo bài viết: Tài liệu thể tích khối đa diện
Tags: #Toán 12
